車輪の踏面勾配と曲線抵抗

このページは、2019年3月に保存されたアーカイブです。最新の内容ではない場合がありますのでご注意ください

おきらく研究室：レイアウトと列車のページ鉄道模型

車輪の踏面勾配

更新履歴’０３／３／７用語を変えました．

はじめに

曲線では外側のレールが内側よりも長いですよね．「図説鉄道工学」（三輪ほか，丸善株式会社）という本には曲線抵抗の筆頭として，長さの違いで起こる滑り摩擦を挙げています．そこで，長さの違いを吸収するために車輪にはテーパー角（車輪の外側ほど，車輪の半径が小さい）がついています．テーパー角のことを踏面勾配と呼ぶそうです．踏面勾配が何度ぐらいあればいいかを計算してみました．車輪を自作される方は滅多にいらっしゃらないでしょうから，直接役に立つことはないと思いますが，私は曲線での走行抵抗を検討したいので，その事前準備として検討してみました．

記号

回転半径差がなく通過できる最小の半径をRとします．車輪関係の記号は図１のように決めます．

図　１　車輪の記号

記号に対応する用語は下の表のとおりです．．

記号

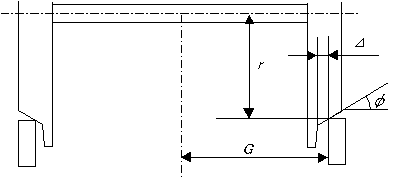
上図の記号

慣用的に用いられる記号

用語

ｒ

車輪半径

ｂ

接触点間距離/2

踏面勾配

フランジ遊間*

*Δ＝[ゲージ　—　（２×チェックゲージ　—　バックゲージ）]／２　です．厳密には，接触点間距離はゲージよりも大きいのですが，車輪形状とレール形状とが決まらないと接触点間距離はわかりません．しかし，レール形状も車輪形状も事実上規定されていませんので，接触点間距離が求まりません．そこで接触点間距離≒ゲージとしました．

さて，ここで車輪が一回転したときのことを考えてみましょう．図２をご覧下さい．初期状態で車輪が北に向いている（車軸は東西に向いている）として，右カーブ（進路を東に変えていく）だとします．

図　２　車輪の進む位置
（注：ゲージは慣例にしたがってｂを使用．図１とは違います）

車輪半径が同じだと図２のように，一回転したとき進む距離が違ってしまいます．そのため，踏面勾配をつけて回転半径差をつけることで，α＝βとなるようにします．この条件を満たす踏面勾配は

です（このページの下に導出過程があります）．

実物の計算例

実物に詳しい方から教えて頂いた数値（文責ははいでにあります）で計算してみました．

在来線

新幹線

踏面勾配(rad)

1/20(=0.05rad)

1/40(=0.025rad)

フランジ遊間(mm)

車輪半径(m)

0.43

0.455

接触点間距離(m)

0.55

0.72

曲線半径(m)

675

2600

この表から，実物では踏面勾配の効果で曲っていることがわかります．

模型の計算例

模型の踏面勾配がよく分からなかったので，曲線半径を既知として計算してみました．

１６番

曲線半径(mm)

６００

車輪半径(mm)

５．４

フランジ遊間(mm)

０．６

接触点間距離(mm)

１６．８(*)／２

踏面勾配

７．２

(*)呼び巾は１６．５ｍｍですが，NMRAのHO線路の規格（＊）では下限値が１６．５ｍｍ，上限値が１７．１ｍｍなので，その中間の１６．８ｍｍを用いました．(＊：http://www.nmra.org/standards/s-3.html)

踏面勾配はだいたい約３°（実物の在来線とほぼ同じ）だそうですから，必要な踏面勾配の半分ぐらいしかありません．模型では回転半径差の補正できないようですね．

今後

曲線での抵抗を計算してみたいと思います．

おきらく研究室：レイアウトと車両のページ　by　はいで　

（付録）踏面勾配の式の導出過程

車輪がカーブの外側に⊿だけ移動したとします．
このときの外側の車輪の半径roは，踏面勾配がついているので

ro=r+⊿φ-------------------------(1)

となります．一方，内側の車輪の半径riは

ri=r-⊿φ-------------------------(2)

となります．

ここでレールの半径を考えてみます．
曲線外側のレールの半径Roは

Ro=R+G-------------------------(3)

曲線内側のレールの半径Riは

Ri=R-G-------------------------(4)

となります．

さて，ここで車輪が一回転したときのことを考えてみましょう．図２をご覧下さい．初期状態で車輪が北に向いている（車軸は東西に向いている）として，右カーブ（進路を東に変えていく）だとします．

図　２　車輪の進む位置
（注：ゲージは慣例にしたがってｂを使用．図１とは違います）

車輪が滑らないとしたときに，曲線外側の車輪が一回転して進む長さLoは

Lo=2πro　( =2π(r+⊿φ) )-------------------------(5)

です．一方，曲線外側のレール半径がRoなので円周は2πRoですから，車輪が一回転することで変わる車輪の進路βは，

β=2πro/(2πRo)-------------------------(6)

です．これを計算すると

-------------------------(7)

となります．ここで，βの意味を再度もうしあげますと，進路が北から方位角βだけ東に変わることを意味します．同様にして，内側の進路角αを求めると

-------------------------(8)

となります．回転半径差がなく車輪転がったら，内輪も外輪も進路角が同じなので，

-------------------------(9)

となります．式(9)に式(7)(8)を代入して踏面勾配φについて解くと

-------------------------(10)

となります．

式の考察

式(10)は無次元の項（r/R, G/⊿)の積になっていることにご注目下さい・

１）車輪の半径と曲線半径との比(r/R)

ｒ／Ｒの値はゲージ・スケールにはあまり依存しません．大雑把に言えば，スケールが２倍かわると，ｒもＲも同じに２倍になるからです．たとえば，実物で直径８６０ｍｍの車輪を考えてみます．１６番では半径が５．４ｍｍ，Ｎでは２．９ｍｍになります．一方，１６番の最小半径を６００ｍｍ，Ｎの最小半径を２８０ｍｍして計算してみました．下の表を御覧下さい．１６番もＮも大体同じですね．でも，１２ｍｍは，１６番よりもゲージが狭いのに曲線の半径が大きいので，ｒ／Rが大きめです．

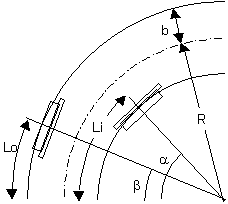
ｒ　mm

Ｒ　mm

ｒ／Ｒ

１６番

５．４

６００

０．００９０

１２ｍｍ

４．９

７３２

０．００６８

Ｎ

２．９

２８０

０．０１０２

上の表から，だいたい

ｒ／Ｒ≒０．００９　　です．

もう少しｒ／Ｒについて考えてみましょう．

車輪の半径ｒが大きいほど踏面勾配が大きくなります．
レールの内外差が１０％あったとします．車輪の径が10mmのものと5mmのものとがあるとしましょう．１０ｍｍ径の車輪の１０％は１ｍｍですから，車輪の半径が１ｍｍの差がつくような踏面勾配が必要です．一方５ｍｍの径のタイヤは０．５ｍｍだけの差がつくような踏面勾配で十分です．１０ｍｍ径も５ｍｍ径も，フランジ遊間⊿が同じだとすれば，踏面勾配が２倍違ってきますよね．

曲線の半径Ｒが小さいほど踏面勾配が大きくなります．
接触点間距離Ｇは一定ですので，曲線の半径が小さくなるほど，内のレールと外のレールとの半径の比が大きくなるからです．

２）ゲージと車輪の厚みとの比（Ｇ／⊿）

Ｇ／⊿も，ｒ／Ｒと同じようにゲージには依存しにくい値のはずです．１６番の車輪と線路をそのままスケールダウンしてＮゲージの車輪と線路を作れば，Ｇ／⊿は一定ですよね．具体例を表にまとめてみたところ，ゲージによって随分違いますね(笑)．

⊿　mm

Ｇ　mm

Ｇ／⊿

１６番（ムサシノモデル）

０．６

８．４　（＝１６．８／２）

１４．０

１２ｍｍ（パブロ　Φ9.5 プレート）

０．２５

６　　　　（＝１２／２）

２４．０

９ｍｍ（ＮMRA規格）

０．０７

４．５　　（＝９／２）

６４．３

上の表から，HOｊから１６番ではだいたい

Ｇ／⊿≒２５　　です．

なお，NMRAの規格は，ノミナル値ではなく，チェックゲージは上限値，バックゲージは下限値です．このため，G／Δが大きいのかもしれません．

注１：ムサシノの規格は右記ＵＲＬから調べました．http://www.musashino-m.co.jp/special/special-1.htm
注２：パブロの規格は森井様のＨＰ（右記ＵＲＬ）から調べました．http://www.morii.jp/railmodel/wheel.html
注３：NMRA の規格は右記ＵＲＬから調べました．http://www.nmra.org/standards/s-4.html

もう少しＧ／⊿について考えてみましょう．

この比は直感的に理解できると思います．接触点間距離の割にフランジ遊間が大きいかどうかという指標です．
接触点間距離が大きいほど内外のレール長さの差が大きくなりますので，踏面勾配が大きくなります．
フランジ遊間が少ないほど，わずかな⊿で車輪の半径差を稼がなければいけないので踏面勾配が大きくなります．スケール通りにしようとしてフランジ遊間⊿を小さくすると，踏面勾配φが（おそらく実物よりも）大きくなってしまうんですね・・・・・・・

実物の計算例（再掲出）

実物に詳しい方から教えて頂いた数値です．文責ははいでにあります．

在来線

新幹線

踏面勾配(rad)

1/20(=0.05rad)

1/40(=0.025rad)

フランジ遊間(mm)

車輪半径(m)

0.43

0.455

接触点間距離(m)

0.55

0.72

曲線半径(m)

675

2600

この表から，実物では踏面勾配の効果で曲っていることがわかります．

模型の計算例（再掲出）

模型の踏面勾配がよく分からなかったので，曲線半径を既知として計算してみました．

１６番

１２ｍｍ

曲線半径(m)

６００

７３２

フランジ遊間(mm)

０．６

０．２５

車輪半径(m)

５．４

４．９

接触点間距離(m)

１６．８

１２．０

踏面勾配

１４．１

１１．０

ＨＯｊの踏面勾配は約３°（実物の在来線とほぼ同じ）だそうですから，必要な踏面勾配の１／３ぐらいしかありません．模型では回転半径差の補正できないようですね．

今後

曲線での抵抗を計算してみたいと思います．

謝辞

稲葉清高さんにフランジ遊間やゲージの規格についてご教示いただきました．たいへん感謝しております．

このページは、2019年3月に保存されたアーカイブです。最新の内容ではない場合がありますのでご注意ください