By　田端機関区 Ｄ５１　さん　　2004/5/12

長い長い貨物列車を牽き、重連で勾配を上ってくる蒸気機関車。その姿の力強さは見るものを圧倒させる。そん な情景を模型で再現できたらと、いろいろな人が苦労してきた。サウンド、スケールスピードと いったリアリティーの追求がまさにそれだ。しかしながら、そのリアリティーも完璧には望めな い。それは模型の制約からきている。たとえば、模型では実物と同じ精度で線路などを作ることは到底不可能であり、その上、狭いスペースの関係から急勾配・急曲線になる。こういった制約の中で実感的に蒸気機関車それも編成列車をいかにして走らせるかを 牽引力という観点から検討してみようと思う。

まず、模型の制限が実物に対して大変にゆるい点を考えてみる。それは機関車の重量である。実物の場合、特に 蒸気機関車にとっての制約で最も厳しかった軸重制限が模型にはないためだ。軸重制限とは車軸 (特に動輪)1軸に乗せられる重量の制限で日本の場合、路盤、レールの関係から東海道本線ク ラスの特甲線(1959年以降は1級線と呼ばれるようになった)でも16t程度でC62形では三軸の動輪上重量が合計で48.2ｔだった。これをＮゲージの日本スケールにあわせて150の三乗で割ると(重量は体積に比例すると考えた上で)14.28グラム となる。つまり、軸重５グラムないということだ。僕はＣ62の模型を持っていないので、模型 との比較のためにＤ51形で見ると実物が軸重14.63tでKATOの模型の場合ス ケール通りならば(KATOの蒸機はオーバースケールで大体1/140ぐらいで作られているので)5.3グラム程度である。実物ではC62 のほうが軸重が大きいのに模型の換算ではD51の値のほうが大きくなっているのはC62を1/150、D51をKATOスケールの1/140で計算しているためで、KATOスケールで C62を計算すると5.8グラム程度となる。ちなみに、これからの表記では縦横高さ1/150を日本スケール(主に客車貨車やワールド工芸などの金属製蒸気機関車模型。体積は、1/(150の三乗)＝1/337500)、縦横高さ1/140をKATOスケール（体 積は1/(140三乗)=１/2744000）、縦横は１/150で高さだけ1/140をマ イクロエーススケール(腰高気味で体積は1/(150の二乗×140)＝1/3150000)、縦横高さ1/160を標準スケール(新幹線・外国など。体積は1/(160の三乗)＝1/4096000)と表記する。一方アメリカでは30tを超える軸重を許容する だけの線路を持っており、有名なところではペンシルヴァニア鉄道のK４(軸配置パシフィック の蒸機)は動輪3軸で96tつまり軸重32ｔで標準スケールでは7.8グラム程度になり日本のとの差を感じられる。

さてここで、Ｎゲージの模型蒸機の軸重 はどうなのだろうか？ちなみに模型の軸重は動輪以外の先従輪を取り外して計った機関 車重量(動輪上重量)を動輪軸数で割ったものである。ここで、KATOスケールのＤ51を 計ってみようと思う。そこで、D51をテンダーつきのまま計りに載せてみると、116グラム と計測された。これはKATOスケールで約318tとなる。これは実物の78.4ｔの約4倍だ。一方、軸重は約21グラム、KATOスケールで58ｔとアメリカの30ｔ級よりも重く、実物の Ｄ51のやはり4倍程度となる。ほかの車両もあとで表にまとめるが、このKATO製 D51はNゲージの車両の中でもかなり重い部類である。
　　なぜ、これほどまで重い車両が普通に模型では走れるのだろうか。その答えは線路と車両重量の縮尺の違いである。今まで車両重量の実物換算に重量と体積が比例すると仮定してスケールの三乗で計算してきたのはお分かりだと思う。一方でその重量を受け る地面は面であり線路の太さも断面積である。もうお分かりだと思うが重量が1/三乗でスケー ル通りなのに対して、それを受ける線路は1/二乗がスケール通りとなっているのだ。つまり、 線路にとってスケール通りの重量で作られた車両の重さは実物のレールが受ける重量に対するとスケール一乗分軽くなるのだ。逆の言い方をするとレールにはＮゲージの場 合、スケール重量の約150倍程度の余裕があるのだ。だから、スケール重量の4倍も の重い機関車が走れる上に真鍮や洋白などの鉄よりやわらかい素材でレールが作れるのだ。しか も、Ｎゲージの線路は大抵オーバースケールのため、さらに余裕ができる。この関係に似たもの で航空機に関する法則を二乗三乗法則という。これは機体が大きくなったり小さくなったりすると空気力は翼面積分つまり約二乗変化し(迎角などの変化は無視)、重量は三乗分変化することである。このように模型にも二 乗三乗法則に近い関係が起きるのだ。

さて、このようなスケールより重い車両が実感的に走るにはそれなりの力が必要となる。さらに、模型には実物 よりきついカーブや勾配、それに伴った走行抵抗の増加がある。さらには車輪の転がりの悪さ、 二乗三乗の法則による線路に対する車両の軽量さから慣性はからきし駄目なことが拍車をかけ る。こんな中で編成列車を走行させるには実物よりも一定機関車重量あたりの動力性能が強力である必要が出てくる。さて、Ｎゲージの蒸気機関車の牽引できる 列車は実物の牽引できる量と相対的に同じなのだろうか？
　　そこで僕の鉄道に在籍する蒸気機関車の中から走行性能が優れていると思われる10台を選んで測定してみ た。ちなみに家にある機関車の両数は14台で、測定に使わなかった4台はナローゲージ風小型 機関車やマイクロエースエース製の高さオーバーの激しいものだ。ここではマイクロエースス ケールの体積換算の不都合があるため(純粋な模型の体積重量比較ができない)同社の小型機を除外し、マイクロエースエース製は傑作と称される3つと古典機(高さのみが高く換算されることはない物)のみとした。測定方法は図１のとおりでいたって 簡単だ。

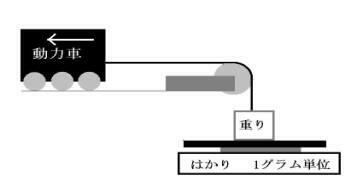図１　実験設備

まず、糸(ミシン糸を採用。たこ糸など数種類の糸の比較の上で一番摩擦ロスの少なかったため)と重りをつな ぎ、はかりに載せ、板に固定した片方の車軸をはずした台車に掛けてそれを滑車として糸を垂直 方向から水平に導き、その糸端と動力車の連結器をつなぐ。そして糸をたるませて重り全重量をはかりの上に掛けた状態で矢印の方向に発車、動力車は糸を引き、空転を始める。そして、2秒 ほど空転して数値が安定してきたところで最初の重りの重量とそのときの数値の 差を読みとる(空転する直前の一瞬は空転後より10グラム近く大きい値を出すことがあるので空転したときを計測した。この一瞬の巨大な値はハンマーで釘をたたいたときに出るような一瞬の力であるた め。)。こうして読み取った値が牽引力だ。具体的な機器のことを言うと、はかりは1グラム単 位ではあるが手紙などのグラムを正確に測るデジタルはかりで、重りの重量は60グラム(N ゲージの牽引力で50グラムに達することはまずないのでこれで十分)、計測時に流す電 流は9Vでこれは模型運転時の最高速度に大体あわせた(文化祭でMAXにして脱線させるような運転は論外)。片軸はずした台車は自作蒸気機関車で使ったKATO 製の余り(集電機能付き)で中空車軸を使い、摩擦を少なくしている。計測は重りの差を測ると いっても実際は重りを乗せた状態ではかりを0にあわせ、糸を引かせたときに表示されるマイナ ス表示を読み取った(一応、マイナスでもはかりが正確に働くかチェック。はかりの箱では±1000グラムまで正確に測れますとのこと)。計測は基本的に三回繰り返し、三回とも誤差 １グラム以内なら三つの中の最低値を取った。基本的にこれで3回とも誤差がほとんど なく計測できたが、1台だけ計測に失敗したものがある。これについては後ほど説明する。さ て、下の表が実際に計った結果だ。

表　１　牽引力測定結果

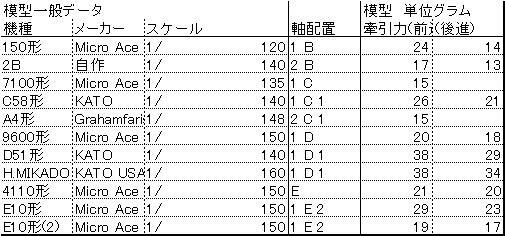後進は重連用カプラーのあるもののみ(一部例外)計測した。こうして見てもただの力比べになってしまうので図２と一緒に見ていただきたいが、とりあえず、表２のみを説明しよう。先ほど出た誤差が大きく出たというのが同じ機関車なのに二つ表示されているE10で (2)のほうの牽引力が極端に弱い。これはゴムタイヤが磨り減っていためで3回計測したとき 誤差は8グラムに達した。どうやら磨り減ってざらざらになり弾力を失ったゴムの表面が空転中 はがれて中のまだ弾力のあるゴムが表面に現れて牽引力を一時的に取り戻したりしたためだと思われる。そのためかE10(2)の計測後は線路に消しくずの様な黒いゴムの粉が見られた(他の車両ではそこまでゴムタイヤが空転で磨耗することはない)。 E10の(１)のほうは５回ほどの(２)の計測のうちに切れたタイヤを交換(片側しか切れな かったが反対側も弱っているので両側とも交換。タイヤはトミックス製。実はマイクロエース エースの蒸機のタイヤはトミックスの電機用で代用できる。KATO製は幅広のため使用できない)したため(２)より１０グラムほど強力で３回での誤差もほとんどなかった。ちなみにE10の前進は逆行正位ではなく一般と同じ煙室側を前とした。
　　さて次の表に入ろう。ここでは動輪上重量に対する性能を考える。

表２　牽引力と動輪上重量

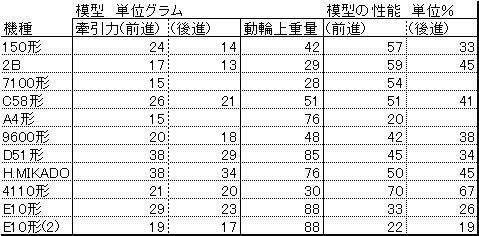上の表における模型の性能とは牽引力/動輪上重量をパーセントで表したものである。数値は表を見ていただく として今はこれらのデータをまとめた下のグラフをいただこう。

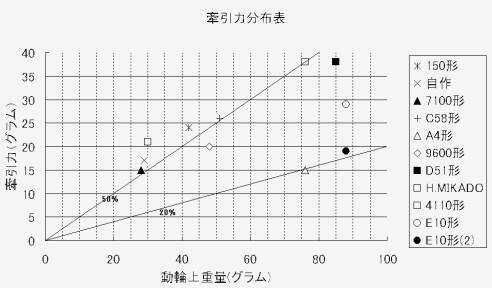図１　動輪上重量と牽引力との関係

これを見ると大体50％ぐらいのところに点が集中している。 これは実物と大変異なるところだ。この模型のグラフを見るとA4とE10(2)が 20％と低く見えるが、A4はゴムタイヤがないのとE10は前述のようにゴムタイヤが機能していない状態での最低値なので仕方がない。むしろ、20％という値は実物とほぼ同じと なっており金属車輪のみを見れば模型においても動輪上重量と牽引力の関係が実物とほぼ等しいといえるのではないか。一方ゴムタイヤで稼いでいる車両 は約30%の分をゴムタイヤだけで受け持っているためタイヤにかかる負担が懸念される。そのため「性能」の%が高くてもよい動力であるとは言い切れない。また、グラフは前進のみを記したが、表のほうを見てもらうと蒸気機関車では後進の方が％が低い。これもやはりゴムタイヤのためで蒸気機関車では前進を基本としているため最後部の動輪両側にゴムタイヤをつけることが多い(ちなみに電車などは前後台車に点対称 に取り付けられることが多い)。そのため前進で牽引するときの重心が後部に来た時のほ うが粘着はよくなる。今まで計測してきた車両の中で9600だけが最後部の動輪ではなく第三動輪(後ろから2つ目)にゴムタイヤが付いて いた。そのため前進後進のゴムタイヤにかかる加重変化が少なく前進後進の％の差が他の形式よ り少なくなっている。これは9600が入換運用など実物でもバック運転の機会が多かったため それを再現できるようになっているためと思われる。また4110、E10も前進と後進の％差が少ないが、これは5軸の動輪中1軸だけがゴムタイヤのため相対的にゴムタイヤにかかる荷重がほかの形式より少なくなり、そのために変化が少ない と思われる。


ここまでの話では模型だけだったが以前に述べた重量の面で模型の重量制限が格段にゆるいことを次の表で再び 確かめてもらおう。

表３　模型と実物の重量の比較

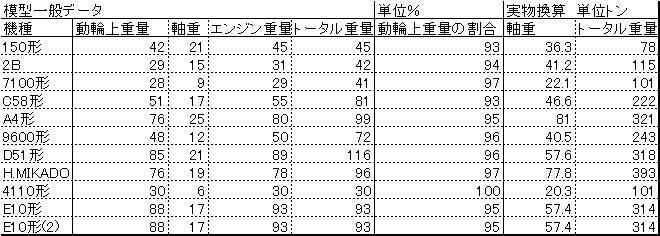スケールは最初の表に表記してあるのでそれを見ていただきたい。まず、軸重(ここだけ有効数字が一桁多いのは実物換算で動輪複数を考慮したため。ほかの有効数字が整数止まりなのははかりが1グラム単位 だったため)は実物換算で大体実物の4倍強ぐらいが普通だ。しかし、実物換算のトータル重量が実物の2倍程度なのだ。中には実物 の1.5倍以下というものもある。これは動輪上重量 の割合が大きいためだ。
　　動輪上重量の割合は動輪上重量/エ ンジン重量を%で表したもの(エンジン重量とはテンダーを除いた重量)で実物で はC62の軽量型が50%と大型機関車ほど%が低くなりやすい(4110 は実物も全軸駆動なので100％)。実物の大型の先従輪つきの機関車では多くても80%程度、普通は60%強で模型より格段に小さい。これは動輪がロッドでつながっているために全軸駆動にできず機関車中央にできる だけホイールベースを短く取ってまとめ、軸重制限でまかない切れない重量を先従輪で負担した ためだ。しかし、模型の場合は軸重制限が甘く、先従輪は脱線しない程 度の重量をかければよいため90%を優に超える数値が出てくるのだ。こうす ると今度は別の問題が出てくる。模型は重量配分が変わっても実物と同じ形をしている。すると 今度は短くまとめられた動輪ホイールベース(エンジン全長の20から30％)だけで機関車のほとんどを支えることになり前後バランスが悪くなる。もし、C62の模型などをお持ちだったら先従輪をはずしてみてほしい。前後が浮かんでい るように見えないだろうか？つまり真ん中の一部で車両全体を支えているのだ。つまり、電車な どの車体両端に台車が着く車両に比べ極端に前後安定性が悪くなる。
　　このような状況では重心位置の設定 が牽引力に響いて来やすい。一般には、動輪全軸の重量配分が同じであるのが望まし い。つまり、模型で軸重(上の表はすべて平均軸重で計算、実物の蒸気機関車の場合は最大軸重 で計算)と表記した数値が1軸あたりにかかって、重量を動輪全軸で均等に支えるのが望ましい はずだ。たとえばHOゲージ以上の車両では車両の牽引力アップに鉛の補充で重量をアップすることが一般的だが、その場合は重心位置に気をつけないと重心がかなり前がちとなり、逆に牽引力が落ちることもあるらしい。しかし、 Nゲージの蒸気機関車の場合は特定の軸にゴムタイヤを履かせているためそのことが違ってく る。ゴムタイヤは金属車輪に比べて格段に滑りにくい。さらにこのゴムタイヤに荷重をかければ さらに滑らなくなる。つまりゴムタイヤのある車軸上に走行中重心がくるようにすれば一 番牽引力が上がるということだ。そのため、ゴムタイヤが最後尾の動輪についているN ゲージの蒸気機関車の場合、重心をかなり後ろにとったほうが牽引力が大きくなる。また、Nゲージの蒸気機関車のほとんどはキャブに大きなモーターを積んでいるため、HOなどのように重心が前がちにな らず、むしろ中央からやや後ろよりにあるのが普通だ。しかし、ゴムタイヤは磨り減ったりして 車輪の精度は金属車輪よりも格段に悪い。そのゴムタイヤに荷重をかけるのは単に重心がゴムタ イヤ上にあるだけでは無理だ。その例としてマイクロエースエースの9600を上げよう。この機関車の重心は第三動輪よりやや前にある。そして第三動輪にゴムタイヤがはまっている。つ まり、大体重心がゴムタイヤ上にある。しかし9600はD形なので第三動輪の後ろに第四動輪 があり、その第四動輪が後ろの荷重を受け持っている。僕の見たところ走行時、客車などから後ろへ引っ張られる機関車は最も滑りにくいゴムタイヤつき動輪とレールの接点を中心にテコの様に前側が上がり気味、後ろ側が下がり気味となり、重量の大半は後ろ側の車輪にかかるようだ。そのときゴムタイヤの後ろに動輪(荷重を受ける車輪なら動輪でなくてもよい)が無ければ後ろに偏った重量すべ てをゴムタイヤで受け持つことになるが、後ろに動輪がある場合は後ろに偏った荷重を後ろ側の 車輪と分散して持つ形となるためゴムタイヤへの荷重は減ることが多く、極端な場合ゴムタイヤが磨 り減って線路に密着せず、ほとんどゴムタイヤが機能してないこともある。そのため前進での牽引力はやや劣るが、前に も述べたとおり逆行でも荷重の変化が少なくできているため全後進の牽引力差が比較的少ない。一方、重量と最後部の動輪についたゴムタイヤで 牽引力を稼いでいるD51は後進の牽引力が極端に落ちている。しかし、9600と違 いゴムタイヤが磨り減っても浮き上がることは無く、逆に金属車輪を浮き上がらせてでもゴムタ イヤが線路に密着するように力が働く。しかし、後進ではそのゴムタイヤが浮き上がりやすくの 牽引力は極端に劣るのである。

このように牽引力についてみてきたが、これから模型を走行させるに当たって一番重要な、「実 物と同じ編成列車」を走らせられるか考えてみよ うと思う。実物 では牽引可能な列車の量を考える基準に牽引 定数というものがある。これはその機関車が10ｔの車両を何両引き出せるか、またはある速度で牽引し続けられるかということを示した値だ。間違えないでほしいのは牽引定数とは牽引力を10tで 割ったものではないことだ。実際実物のC62でも牽引力はわずか19ｔしか ない。しかし数百トンの列車を平坦線で牽引できる。これは列車を動かすための力が列車の総重 量に比べてきわめて小さいためである。実際、10トンの貨車を人が一人で勾配が無ければ牽引可能といわれている。実物の場合、平坦な場合、プレーン軸受け(メタルによる軸受け。旧型車両に用いられる。)で車両重量の0.７%以下、コロ軸受け(ローラー ベアリングによる軸受け。現在使用されている車両のほとんどがこれを用いている。)で 0.3%程度だという。昔はプレーン軸受けが主流だったため操車場内の勾配は3‰以下という 基準だった。これは3‰つまり車両重量の約0.3%の力と風などの力が掛かってもプレーン軸受けは転がりださないから設けられた基準だ。0.3%に「約」をつけたのは勾配の表現「‰」は勾配の角度のタンジェントであるのに対して、勾配上で車両が斜面と平行に受ける力は車両重量×勾配の角度のサインとなるためだ。ただ、一 般の鉄道の勾配では角度が極めて小さいため水平方向の距離とレール上の距離がほとんど同じなので、 車両にかかる力ともおおよそ一致するのだ。このように勾配上では車両重量の勾配と同じぐらいの力が走る方向にかかる。ここから分かったと思うが牽引定数は勾配によって変化する。同じ牽引力でも勾配上では付随する列車から機関車にかかる力が違ってくるからだ。蒸気機関車の末期、室蘭本線ではD51形(一般には1000t牽引と言われるが勾配が10‰以下の線区では1150ｔ持たされる のが常だったという)単機で常識をはるかに超えた総重量2400tの石炭列車を走らせてい た。石炭の貨車はプレーン軸受けなので2400tの0.7%、それに発車抵抗の分を考えて0.8％として、勾配が無い区間で牽くために必要な力を計算すると11t程度となる。これはあくまで勾配がまったく無い場合な ので現実ではこれの1.5倍程度必要になるだろう。しかし室蘭本線には数‰の上り勾配しかな いので可能だったのであって、もし25‰の線区だったらわけが違う。25‰の区間では列車は 常に車両重量の2%強が坂の下のほうへ向く力としてかかっている。つまり、車両が元から持っている抵抗に加えて勾配抵抗がかかり、プレーン車軸の場合トータルで牽引に必要な力は車両重量の3%以上になる。つまり、平坦線と勾配線では数倍の牽引定数の違いが出てくるのだ。


ここまでは牽引定数つまり機関車の引っ張れる最大の列車重量を話してきたが今度は列車の定数に入る。簡単に言ってしまえば機関車の牽引定数より列車 の定数が少なければその列車をその機関車が引けるということで、逆に言うとある線区で 列車の換算定数何車分の列車を引けるかをその機関車のその線区における牽引定 数としているのだ。実物の機関車列車の場合、出発前に列車の定数が通知される。たと えば上越線のＳＬ奥利根号の場合は「現車6車　換算21.5車(21車半)」となる。これは客車が6両で210ｔという意味だ。換算は単純に列車重量を10ｔで割っただけであるた め軸受けの種類や勾配によって必要な牽引力は変わってくる。また、列車の定数には積車重量(客や貨物が乗っている状態)と空車重量があって、上の換算は積車重量となっている。奥利根号の場合、12系客車が用いられているので編成の 内訳はオハ12が2両にオハフ13が3両、スハフ12が1両となり、換算するとオハ12とオハフ13が空車3車・積車3.5車、スハフ12が空車3.5車・積車4車となるのだ。一方、その列車を引くD51形の牽引定数は上越線の高崎〜水上で100車ほどあり余裕たっぷりということになる。


さてここから、模型の牽引定数の話に入 る。模型の場合軸受けにはパブローラー車輪を除いてコロは用いられず、大抵はピボッ ト軸受けかプレーン軸受けだ。ピ ボット軸受けとは車軸先端を尖らせて先端の一点で回転軸を支えることで軸受け内の摩 擦を減らすように作られた軸受けでＮゲージでは最も一般的な軸受けの形態だ。しかし、このピボット軸受けも実物の軸受けに比べて精度が悪いため、一点のみで回転軸を保持することになら ず軸の側面で保持することになり、実質プレーン軸受けと同じになっている。それでも本当のプレーン軸受けよりは摩擦は少ない。力学のクーロンの法則で摩擦は見かけの面積に関係せず、重量だけに左右されると習ったのでプレーン車軸とピボット車軸の軸 受けの面積の違いは重量が同じなら摩擦とは関係ないはずだ。しかし、実際は軸受け内の微妙な引っ掛かりが多数あるため当たる面積が広いほどこの引っ掛かりが多くなり力学の理論とは反する結果 になる。話がやや脱線するがこれと同じことが動輪の軸数にも関係する。実物の場合は軸重制限が厳しいので動輪軸数が多いほど粘着重量を増やせるため動輪と線路の摩擦が大きくできる。これは理論と一致するがとある HOゲージの運転会で貨物列車を走らせたとき動輪3軸のＣ57では牽引できなかった列車をそ のＣ57より軽い動輪4軸の9600が軽々と牽引できたという。もちろんＮゲージのようにゴ ムタイヤのような特殊なものは使っていない。話を元に戻すとＮゲージを走らせるにあ たって重要なのは精度のよいピボット軸受けということになるだろう。
　　さて、このピボット軸受けはどれぐらいの転がりを実現できるのであろうか。残念ながら実物のプレーン軸 受けの最低ラインにも届かない車両が多数あるのが現状だ。とあるホームページから調べるとＮ ゲージのトレーラーの牽引に必要な力は車両重量の0.7%程度の実物並から5%までばらつ き、平均では2.5%程度だという。実際実験でも大体その程度の値がでたのでほぼ正確だといえるだろう。これを元に模型の蒸気機関車の牽引定数を下の表にまとめる。模型の牽引定数では10ｇ を1車と換算した。10gは大体模型のワム80000形２軸貨車の重量で実物でも約 10tとほぼ実物の定数と同じなのが好都合だからだ。表４には直線と曲線の牽引定数が平坦線 と勾配線で書かれている。曲腺の牽引定数を書いた理由は模型が実物に比べてきついカーブを走っているために曲線抵抗が大きくかかわってくるためだ。具体的には直線に対して半径250ミリのカーブは抵抗 が車両重量の1%ふえる。実物ではカーブ半径が100メートルきつくなると車両重量の0.1%抵抗が増えるという。

表４　平坦・勾配・曲線路における牽引定数

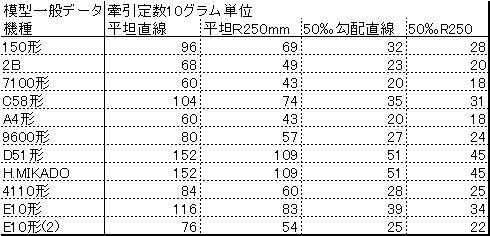さて、この表に照らして考えてみよう。ここではテスト用線路として任意の勾配が作れる長さ2ｍの直線を用意 した。牽引に使うのは全車両35g(3.5車)に統一させた12系客車と適当に混ぜた貨車の2編成だ。それぞれフル編成で換算35車・40車となった。D51とHeavy Mikadoは両方の列車を60‰区間で牽引可能だった。勾配を60‰に設定したのは50‰プラス曲 線抵抗に近い値を出すためだ。実際は60‰で計算すると抵抗が50‰プラス曲線より多くなる ため、この区間を走れれば50‰曲線区間で余裕を持って牽引できるということになる。一方ほかの車種では大体上の数値に等 しい値を示した。ただ、貨物列車は軸数が多い分、抵抗が大きいようでやや計算値より少 なくしか牽引できないものも見られた。平坦にするとどの機関車も軽々と換算40車の貨物列車を引くことができた。このように考えるといかに勾配が列車の走 行の抵抗になるかが分かる。また、いい加減な計測であっても実際に試してみてその結果が計算 値と一致したことから今まで考えてきたことが正しいことも実証できた。実験結果から思ったこ とはレイアウトでの最大勾配を40‰以下(勾配と曲 線の抵抗が合わさっても50‰直線走行程度の抵抗ですむ)に設定し客車など20ｍ程度のボギー車は現車1車・換算４車で計算してあげれば余裕を持って走行可能ということだ。

さて今回は秤を使ってスタンディングスタート形式で牽引力を計測したが、最後の実験で行ったような任意の勾 配が作れる直線を用意し、機関車が走行不能になる最急勾配を測定することでその勾配のサイン を求め機関車の自重に掛け合わせて牽引力を求める方法もある。これの難点は重心が勾配のきつ さによって変化してしまうため今回のような蒸気機関車の場合ゴムタイヤへの加重が変わり、牽引力が変わってしまう恐れがあることだ。しかし一方で正確なサインの値さえ求めればもっと正確に0.1g単位でも計測ができる強みもある。こう いった方法も試行錯誤をして試してみてもいいと思う。

最後になったが牽引力は走る模型の大切な基準であることを感じていただけただろうか。本来ならば曲線抵抗な どももっと詳しく半径別に計測したり、最小通過半径なども調べたりすべきだったかもしれない が、今回の実験程度でも走る模型の性能について知ることができたことに意義があると思ってい る。


参考文献

http://shazba.hp.infoseek.co.jp/page019.html (「おきらく研究所」　はいで氏)

RM　MODELS　温実模知のすすめ(斉藤晃氏)




（'04/5/12はいでコメント）
田端機関区Ｄ５１さん，素晴らしいレポートをありがとうございます．斎藤晃さんがＲＭＭで連載されている 「温実模知のすすめ」のＮゲージ編といった，実物の情報を元にした研究内容に脱帽いたしまし た．田端機関区Ｄ５１さんは，かなりの力学的センスをお持ちの方だとお見受けいたしました．
　　ご投稿頂いた原稿はワード形式で，とても読みやすいものでした．しかし，ＨＰにアップするにあたって， 横長ディスプレイによっては読みにくいこともあるかと思い，一部改行や，太字・赤字による強 調をさせていただきました．原文の趣が再現できなかったことを，田端機関区Ｄ５１さんおよび 読者の皆様にお詫びいたします．

---