緩和曲線とは?
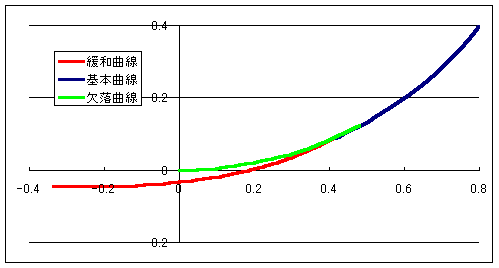
直線からカーブ(円弧)に入るとき,いきなりその半径に突入しないで,直線(半径無限大)から徐々に半径を小さくしていく曲線 です.
下の図の赤い部分です.
実物では,実物での効能は
・脱線防止
・軌道に局部的な負荷を与えない.
・乗り心地の向上
などです.模型でも,効果があります.それは,直線から急カーブに入ると,急に「カクン」と曲がるようにみえますが,この現象を低減できます.
また,脱線防止にも効果があるとの記事を読んだことがあります.
緩和曲線の特徴
鉄道工学の本を読むと,本来はクロソイド曲線(*)で,簡易的には3次関数(y=a x^3)を使うそうです.
そこで,3次関数による緩和曲線の設計ツールを作ってみました.フレキシブル線路でレイアウトを製作される方は,ぜひご活用下さい(責任はとれませんが).
こちらで計算できます. ご自由にお使い下さい(責任はおとりできません.また商用でのご使用は禁止いたします).
(*)大雑把にいうと,レーシングカーがカーブに突っ込んでいくときの軌跡です.
(横)加加速度一定≒ハンドルを切り込む速度が一定〜〜のときの軌跡なんです.
ここで,注意したいのは,クロソイド曲線は(横)加加速度をいくらかに指定しないと形状が決まりません.
その値の設定ノウハウがないので,ノウハウ不要の3次関数をここでは扱います.
3次関数の緩和曲線を調べてみると次のようなことがわかりました.
・半径一定の本来の曲線に合流するとき,約24°向きを変えている.
・緩和曲線の全長は,(本来の曲線の)半径の約0.7倍です.
緩和曲線の長さ
緩和曲線の長さは車両の何台分なのでしょうか. 最小通過半径は車両全長の1.8台分が相場です .その0.76倍が緩和曲線の長さなのですから,大雑把には
緩和曲線の長さ
=車両全長×1.8×0.76
≒1.4×車両全長
となるので,緩和曲線の長さは車両の1.4台分です.ちなみに,実物では最急で300Rぐらいなので車両の15台分です.その0.76倍だと11.4両分です.じわじわと曲げているんですね.模型の最急曲線の円一周は,車両約8.5両分です.実物と比較しないほうがよさそうですね.
【私見】TOMIX線路やユニトラックでの緩和曲線
この節では,私の私見を紹介します.あくまでも私見であり,定説でも確立された技術でもないことを,あらかじめお断りしておきます.
TOMIX線路やユニトラックでは,フレキシシブル線路がありませんので,私は,半径一定の円で近似してみました.つまり,「緩和曲線の長さ(=本来の曲線の半径の0.7倍の円弧)」で「24°向きを変える」円です.この円の半径を計算してみると,本来の曲線の半径の約1.66倍です.
したがって,R280の場合,R470になります. TOMIXにはR541が,KATOのユニトラックにはR481ありますので,これが丁度よさそうだと考えました.ただし,角度は15°です. スペースに余裕があれば2本,余裕がなければ1本,と私は考えました.R541の1本の長さは20m級車両の全長の0.95台分ですのでぎりぎり使用可能?といったところですが,私のレイアウトでは,巾方向に余裕がないので,R541の1本使いにしました.
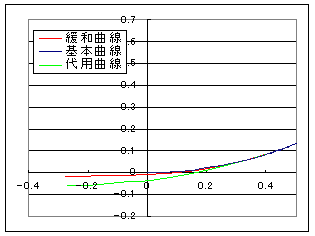
ここで「巾方向に余裕」についてご説明いたします.代用曲線の計算結果を下図にしめします.なおこの半径は1で表示してありますので,目盛りの「0.1」は「0.1×R」を意味しています.