鉄道模型おきらく研究室：レイアウトと列車のページ

おきらく研究　曲線での走行抵抗

はじめに

曲線で牽引力が低下するとよく耳にします．そこでトレーラーの走行抵抗を測定してみました．

測定車両

トレーラー１６両を測定しました．

測定法

試験風景です

トレーラを載せた線路を傾けます．車両が静止できる最大勾配を測定します．

最大勾配では，坂に沿って車両をひっぱろうとする重力と走行抵抗とが釣り合っています．

したがって，勾配の角度をα（rad)とすると

α＝走行抵抗力／重量

の関係があります．

線路はＴＯＭＩＸを使いました．半径は次のとおりです．

・直線

・Ｒ２４３

結果

そこで，勾配法で計ってみました．線路を傾けても動き出さない最大の勾配の角度（rad)が抵抗係数になります．

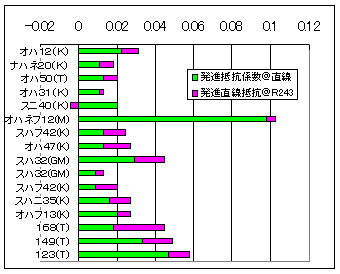
図１　走行抵抗係数測定結果 （参考図）線路を傾けても動き出さない最大の勾配の角度（rad)の直線と曲線における比較： 横軸は直線での走行抵抗係数，縦軸は曲線（R243）での走行抵抗係数．

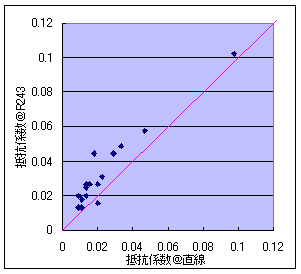
図２　直線と曲線での走行抵抗の比較 （参考図）線路を傾けても動き出さない最大の勾配の角度（rad)の直線と曲線における比較： 横軸は直線での走行抵抗係数，縦軸は曲線（R243）での走行抵抗係数．

もう一度，直線での結果です．これは平坦な直線での発進抵抗係数に相当します．

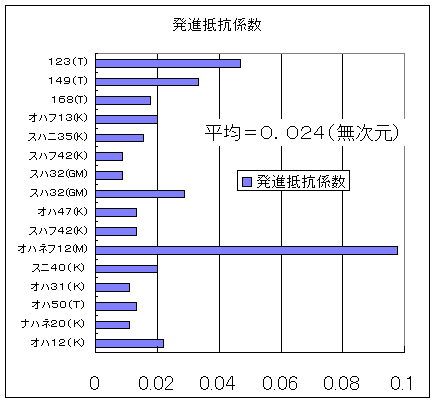
図３　発進抵抗係数（走行抵抗係数）： 直線上での走行抵抗の目安は０．０２４です．

ここで

発進抵抗係数＝発進抵抗／車両重量

です．上図から発進抵抗係数の平均は０．０２４でした．そこで，丸めて

標準的な発進抵抗係数＝０．０２５

が目安でしょうね．

次に曲線での発進抵抗係数です．R243での発進勾配をもとめて，直進での発進勾配との差をとると，曲線での抵抗分が求まります．直線と曲線との発進抵抗の差分だけを表示します．

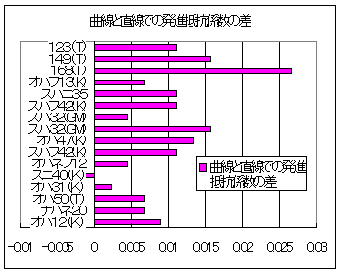
図４　発進抵抗係数（走行抵抗係数）： 曲線と直線上での走行抵抗の差の目安は０．０１です．勾配に換算すると１％相当です．

上の図の平均値は０．００９４ですので，曲線での走行抵抗（R243)と直線での走行抵抗との差の目安は０．０１ですので，勾配に換算すると１％に相当します．

ところで，任意の曲線半径での抵抗を計算するために，曲線抵抗係数を求めます．実物では，曲線抵抗は曲線半径に反比例するそうです．そこでこの値を曲率（＝1／２４３ｍｍ）で割って「曲線での抵抗の増加率」をもとめました．この結果を下図にしめします．

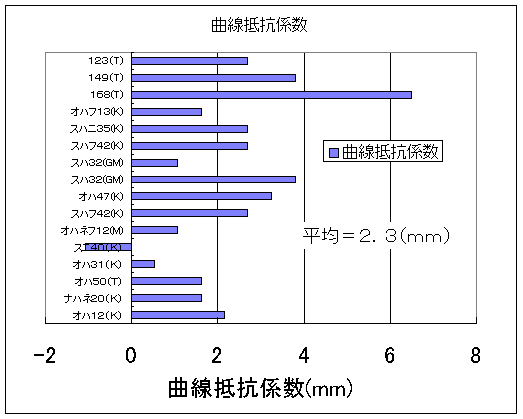
図６　曲線での抵抗増加 曲線抵抗係数の平均は２．３ｍｍです． が，この程度のデータのバラツキなら，丸めて２．５ｍｍとしたほうが良いと思います．

上の図の曲線抵抗係数の平均は２．３ｍｍです．そこでキリよく２．５ｍｍに丸めました．

ですから，２５０Rを走行したことによる走行抵抗は車両重量の１％分で，これは勾配１％分に相当します．

寄り道コーナー 専門書によると実物の曲線抵抗係数は 曲線抵抗係数＝０．６〜０．８ｍ／曲線半径（ｍ）だそうです（１）．ゲージ比で見るとＮゲージのほうが抵抗係数が小さいですね． Ｎゲージ ２．３ｍｍ／　９ｍｍ＝０．２６ 実物 ０．７ｍ／１．０６７ｍ＝０．６６ （１）天野ほか，図説鉄道工学Ｐ１１０，丸善出版，平成４年