| 星の移動に関する、メモ |
注意事項
この項での計算は、使用した数値の桁数が多いので一見は正確そうに見えるが、実際は詳細計算に必要な事項を省略しているので、空を見ながら、1時間後にはあの辺りだろう、とか、明日のこの時間にはあの辺りだろう、とか、来月の今頃はあの辺りに見えるだろう、などと「頭の中でイメージする大雑把な目安」以上の精度は無いので悪しからず。
いろいろ的にはあくまでも大雑把な目安。
まあ、倍から半分程度の誤差はOK! っていう程度の目安。
※ なお、本項における星あるいは月の移動に関しては天の赤道(あるいは白道)を基本として記述しているので、地平の方位(磁針による方位)とでは、本当に倍と半分の差が生じていた。
|
①星(恒星)が1時間当たりに移動していく速度
星(恒星)は天の赤道上を、時計の短針の半分の速度で東から西へ回っていく。 つまり2時間で時計短針の1時間分進む。
(恒星は、天の赤道上で考える。 天の赤道とは、地球の赤道面を天球にまで延長し、天球上に交わってできる大円のことで、恒星や惑星の天球上の位置を決める基準)
星空は毎日、24時間 (正確には1恒星日 23.9345 時間) で一周するので、24時間で1周する時計をイメージする。
今見えている星の、1時間後の位置は、24時間時計の1時間分、通常の12時間時計ではその半分の時間(30分)後に時計の短針が進む角度(15度)だけ、移動する。
※ 1時間当りの移動量= 360 / 23.9345 = 15.04 (度)
また、1分では約 0.25度移動する。 (1度あたり4分で移動する。)
※ 1分当りの移動量= 360 / (23.9345*60) = 0.2507 (度)
月の視直径は約 0.5度なので、約2分で月の視直径分移動してしまう。
(注!) ここでの記述は天の赤道を基準。 地平の方位では倍と半分の差が生じます!
②星の一か月後の位置
今見えている星は1か月後の同じ時間には、天の赤道上で、時計の短針1時間分の角度だけ進んだ位置に見える。
星空は1年で一周(360度)するから大雑把に略算して、1か月あたり、360/12で30度進んでいく。 ちょうど12時間で一回りする普通の時計の、短針1時間の角度に相当する。
①と②より、今、見えている星は1か月後なら、今より2時間早い時刻に同じ位置に見える。
(注!) ここでの記述も天の赤道を基準にしています。 地平の方位では倍と半分の差が生じます! ③一週間後の月の位置
一週間後の同じ時間の月の位置は、約90度東となる。
(月は、白道上で考える。 白道とは、天球上の月の軌道。)
月はおよそ1か月で一周する(正確には公転時間は27日と7時間 42.7分 (27.3213日) なので、
また大雑把に公転周期を28日≒4週間とすれば 4週間で360度移動する事になるから、1週間ではその1/4で90度分遅れる。(見掛け上、東に移動した位置に見える。)
※ 1日当りの平均移動量= 360 / (27.3213) = 13.18 度 、 1週間では= 13.18 * 7 = 92.24 ≒ 90 度
ただし、地平の方位(磁針の方位)でみると、実際の1日当りの移動量(方位の増分)は次の表のように、南中辺りにある時は早く、東西にある時は遅く見える。
(国立天文台HP>暦計算質>こよみの計算による、 2011.09.06-09.18 での計算値。 時刻は 00:00 )
| 日付 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | | 方位 | 248.8 | 242.3 | 236.1 | 229.8 | 222.7 | 214.3 | 203.6 | 189.3 | 170.4 | 148.0 | 126.6 | 109.7 | 97.2 | | 方位の増分 | 7.2 | 6.5 | 6.2 | 6.3 | 7.1 | 8.4 | 10.7 | 14.3 | 18.9 | 22.4 | 21.4 | 16.9 | 12.5 |
④1時間後の月の位置
1日あたりでは、360度/27.3213日で、1日あたり平均約 13.18 度、 1時間にすると、13.2/24=0.549 度分、周囲の星より遅れていく。
月の視直径は約0.5度だから、月の移動は恒星より、毎時、およそ月の直径程度分づつ遅れていく。 (平均した目安。)
また月自体は、天の白道上で一時間当り平均15度弱、つまり2時間で時計短針の1時間分程度進む。 ※ (360-13.18)/24 = 14.45 度
ただし、地平の方位(磁針の方位)では実際の1時間当りの移動量(方位の増分)は次の表のように、南中あたりで最も早く、東西では遅く見える。
(国立天文台HP>暦計算質>こよみの計算による、 2011.09.09-09.10 での計算値。 月齢11.2-11.7 )
| 時刻 (時) | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | | 方位 (度) | 115.8 | 125.9 | 138.2 | 153.1 | 170.8 | 189.7 | 207.5 | 222.7 | 235.2 | 245.6 | 254.7 | 263.2 | 271.7 | 281.1 | | 方位の増分 | 8.8 | 10.1 | 12.3 | 14.9 | 17.7 | 18.9 | 17.8 | 15.2 | 12.5 | 10.4 | 9.1 | 8.5 | 8.5 | 9.4 |
※視界の中心にセットした星が、視界の端から逃げてしまうまでの時間
実視界8.8度のニコン8X30EⅡなら18分ほどは連続して見られる。
※ 実視界 8.8 度/0.2507 度 ÷ 2 = 17.55 分 (中心から端までの移動時間)
実視界5度のニコン12X50では10分。
※ 実視界 5.0 度/0.2507 度 ÷ 2 = 9.97 ≒ 10分 (中心から端までの移動時間)
またフィルードスコープ(ビクセン ジオマ ED67) を30倍(GLH30)で使用した場合、実視界2度なので、4分。
同じスコープで80倍(GL80)を使用した場合には実視界0.7度なので平均約1.4分で視界から消えてしまう。
|
|
天の赤道での移動角度と、地平の方位角との差異について
お星さま(恒星)は北極・南極を軸とした地球の自転に伴って、天の赤道上を定速で動いていく。 (はず)
しかしこの軸は、今立っている地面とは緯度の分だけ傾いているために地平上の方位とでは大きな差があり、頭の中がごちゃごちゃになってしまったので、少し考えてみた。
これであってるのか、間違ってるのか、 よーわからんけど、少々間違ってても自分で納得できりゃいいって事で・・・。
※ 赤緯・赤径から、方位・高度へ変換するには・・・ ははは・・・私には難しくて、まだよーわからん。 (^。^)y-.。o○
| 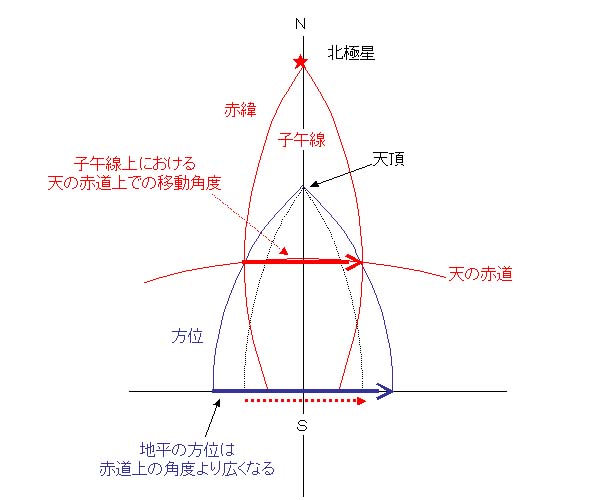 |
南向きの場合(天の子午線辺りの場合)
天の赤道上で星が移動した距離(角度)は、
天頂から降りてくる地平の方位線が開いてくる途中で、地平に達した時には赤道上の方位より大きく開き、自宅の緯度では50%程も広がって見える。
天の赤道上の距離(角度)
< 地平での距離(地平の方位角) となる。
(・・・のかな?) | | 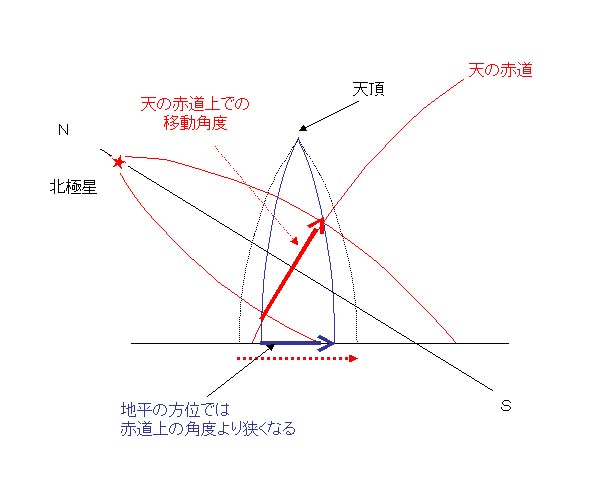 |
東の空 (西も考え方は同じ)
東(あるいは西)の空では、丁度天の赤道の立ち上がりとなるため、星は斜め上に向かって移動する。
このため、地平の方位(地平方向のベクトル)に直すと、天の赤道での移動距離(角度)より短くなり、
天の赤度絵上の距離(角度)
> 地平での距離(地平の方位角) となる。 |
|
|
| 望遠鏡のアイピースと、星の視界内ご滞在時間 |
○アイピースの倍率と実視界、および視界内通過最短時間の簡易計算
○他のページ(「天体望遠鏡」→「生意気にもタカハシFS−60Q」のページから移築・・・ (エラーがあったら、笑って済ませてください!)
注意事項: 1恒星日=23時間56分4.09秒 として、天の赤道上にある星の移動速度(=最大値) を計算した (・・・つもり?)
|
|
| |
|

|