第１章　利用者便益の定義式

■仮定及び前提条件

　仮想的な都市Ｘ市とＹ市を結ぶ鉄道が存在する。

　ＸＹ間には他の交通機関が存在しないものとする。

　ＸＹ間の所要時間は80分とする。現行の運賃は 2,000円とする。

　またＸＹ間の現行の利用者数は１日あたり20,000人とする。

　利用者の平均的な時間価値は50円／分とする。

　需要曲線Ｄは下記のとおり仮定する（※）。

　　　ＱＣ＝Constant（定数）
　　　　Ｑ：ＸＹ間の鉄道利用客数
　　　　Ｃ：ＸＹ間の鉄道での移動にかかる一般化費用
　　　　　　→現状では　運賃 2,000円＋80分×50円／分＝ 6,000円

　※：ＸＹ間には鉄道しか存在しないとの仮定を置いたため、ＱＣはこの定義になる。
　　　ＸＹ間に複数の交通機関が存在する場合には、ＱＣは下記の定義となる。
　　　　Ｑ：ＸＹ間の総利用者数
　　　　Ｃ：ＸＹ間の移動にかかる全交通機関を総合した一般化費用
　　　複数交通機関が存在すると、このＣを求めるためには、数学的に極めて複雑な処理が必要である。
　　　そのため、「ＸＹ間は鉄道のみ」と状況を単純化した。

■利用者便益の定義式

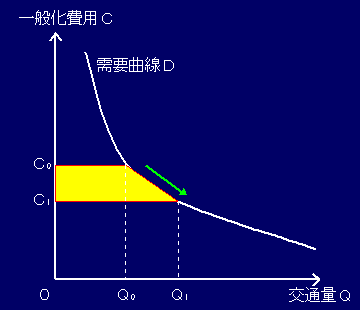
　プロジェクトを実行時の利用者便益（消費者余剰）は下記のとおり定義される。

　　　Ｐi ＝（Ｃi−Ｃ0）（Ｑ0＋Ｑi）／２
　　　　Ｐ　：プロジェクト実行後の利用者便益総額
　　　　Ｃ0 ：現状でのＸＹ間の移動にかかる一般化費用
　　　　Ｃi ：プロジェクト実行後のＸＹ間の移動にかかる一般化費用
　　　　Ｑ0 ：現状でのＸＹ間の利用者数
　　　　Ｑi ：プロジェクト実行後のＸＹ間の利用者数

　この定義式は、（Ｑ0,Ｃ0）(Ｑ1,Ｃ1)（0,Ｃ1）(0,Ｃ0)を４頂点とする、台形の面積を求めていることから、「台形公式」または「ショートカット公式」と呼ばれている。

　プロジェクト実行前の鉄道の収入は、下記のとおり定義される。

　　　Ｉ＝ＦＱ
　　　　Ｉ：鉄道の総収入
　　　　Ｆ：ＸＹ間の運賃料金

　　　Ｉ0 ＝　2,000×20,000 ＝　4,000万円／日

元に戻る

先に進む