第２章　ケーススタディ

■プロジェクトの設定

　ＸＹ間の所要時間短縮を図るプロジェクトを実行することとする。

　所要時間短縮幅は20分とする。

　このプロジェクトは外生的に実行され、実行後の鉄道運行コストは増えないものとする（増収＝増益とするための単純化）。

▼ケース１：

　プロジェクト実行後、ＸＹ間の移動に特別料金 1,000円を課金する。

　　　Ｑ1Ｃ1　＝　Ｑ1×（2,000円＋60分×50円／分＋1,000円）
　　　　　　　＝　Ｑ1×6,000円
　　　　　　　＝　Ｑ0×6,000円

　　∴Ｑ1 ＝ Ｑ0 ＝ 20,000人

　　　Ｐ1 ＝（Ｃ1−Ｃ0）（Ｑ0＋Ｑ1）／２
　　　　　＝（6,000−6,000）（20,000＋20,000）／２
　　　　　＝ 0

　ゆえにこのケースでは、利用者便益が発生しない。

　　　Ｉ1 ＝（2,000＋1,000）×20,000　＝　6,000万円／日

　　　Ｉ1−Ｉ0 ＝ 6,000−4,000 ＝ 2,000万円

　ゆえにこのケースでは、鉄道会社は１日あたり 2,000万円の増益となる。

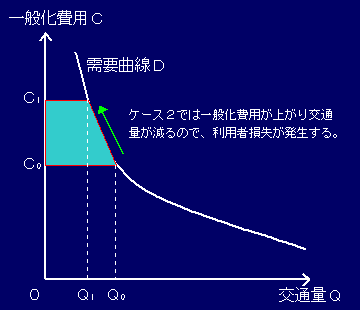
▼ケース２：

　プロジェクト実行後、ＸＹ間の移動に特別料金10,000円を課金する。

　　　Ｑ2Ｃ2　＝　Ｑ2×（2,000円＋60分×50円／分＋10,000円）
　　　　　　　＝　Ｑ2×15,000円
　　　　　　　＝　Ｑ0×6,000円

　　∴Ｑ2 ＝ Ｑ0×6/15 ＝ 8,000人

　　　Ｐ2 ＝（Ｃ2−Ｃ0）（Ｑ0＋Ｑ2）／２
　　　　　＝（6,000−15,000）（20,000＋8,000）／２
　　　　　＝ −1.26億円／日

　ゆえにこのケースでは、１日あたり1.26億円の利用者損失が発生する。

　　　Ｉ2 ＝（2,000＋10,000）×8,000　＝　9,600万円／日

　　　Ｉ2−Ｉ0 ＝ 9,600−4,000 ＝ 5,600万円

　ゆえにこのケースでは、鉄道会社は１日あたり 5,600万円の増益となる。

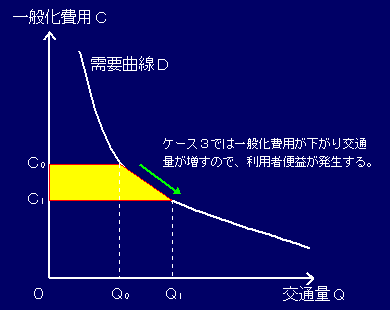
▼ケース３：

　プロジェクト実行後、ＸＹ間の移動に特別料金を課金しない。

　　　Ｑ3Ｃ3　＝　Ｑ3×（2,000円＋60分×50円／分）
　　　　　　　＝　Ｑ3×5,000円
　　　　　　　＝　Ｑ0×6,000円

　　∴Ｑ3 ＝ Ｑ0×6/5 ＝ 24,000人

　　　Ｐ3 ＝（Ｃ3−Ｃ0）（Ｑ0＋Ｑ3）／２
　　　　　＝（6,000−5,000）（20,000＋24,000）／２
　　　　　＝ 2,200万円／日

　ゆえにこのケースでは、１日あたり 2,200万円の利用者便益が発生する。

　　　Ｉ3 ＝ 2,000×24,000　＝　4,800万円／日

　　　Ｉ3−Ｉ0 ＝ 4,800−4,000 ＝ 800万円

　ゆえにこのケースでは、鉄道会社は１日あたり 800万円の増益となる。

▼ケース４：

　プロジェクト実行後、ＸＹ間の移動に特別料金 500円を課金する。

　　　Ｑ4Ｃ4　＝　Ｑ4×（2,000円＋60分×50円／分＋500円）
　　　　　　　＝　Ｑ4×5,500円
　　　　　　　＝　Ｑ0×6,000円

　　∴Ｑ4 ＝ Ｑ0×60/55 ＝ 21,818人

　　　Ｐ4 ＝（Ｃ4−Ｃ0）（Ｑ0＋Ｑ4）／２
　　　　　＝（6,000−5,500）（20,000＋21,818）／２
　　　　　＝ 1,045万円／日

　ゆえにこのケースでは、１日あたり 1,045万円の利用者便益が発生する。

　　　Ｉ4 ＝（2,000＋500）×21,818　＝　5,455万円／日

　　　Ｉ4−Ｉ0 ＝ 5,455−4,000 ＝ 1,455万円

　ゆえにこのケースでは、鉄道会社は１日あたり 1,455万円の増益となる。

元に戻る

先に進む