さて、いかにこういう平面四配位構造を炭素でつくるかという話です。実際の合成的アプローチはいろいろ面白い歴史があるのですがそれは別の機会に譲るとして、今回は本当にこういう構造は実現可能なのだろうかという理論的なアプローチをご紹介します。
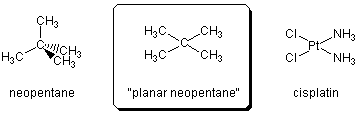
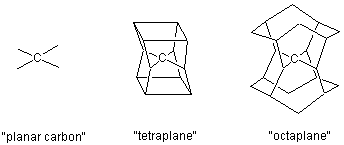
　ネオペンタンそのものを平面にするのは不可能ですから、なんらかの置換基をつけて無理やり中心炭素を平らに固定してしまうことを考えます。たとえば平面ネオペンタン構造の上下に シクロブタン 環をおいて、その各頂点とネオペンタンの4個のメチル基をつないでみましょう。こうしてできたのが"tetraplane"です。図で描くのは簡単ですがこれはいかにも窮屈そうですから、上下の環を少し広げてシクロオクタン環にすると"octaplane"になります。これが今回の出発構造です。ちなみに、こういう一連の同族体を"alkaplane"といいます。

　平面メタンは正四面体メタンより520 kJmol^-1不安定と計算されています。メタンのC-H結合の開裂エネルギーはこの値より約100 kJmol^-1小さいので、メタンは平面に押しつぶされるより先に分解してしまいます。ネオペンタンではこの平面化エネルギーは880 kJmol^-1にも達します。
　"octaplane"の ab initio計算 では、安定 配座 における中心炭素の結合の平面からのずれ（δ）は5.1°で、炭素あたりの ひずみエネルギー は63kJmol^-1だそうです。かなり平面には近いもののまだまだですね。ただ、エネルギー的にはこれくらいの値なら実際に合成されている高ひずみ分子と同レベルです。

　実際の"octaplane"分子は、図のように元のネオペンタンのメチル炭素のところが メチン になっていて、その水素がねじれて配位しています。ここを動けなくするために 四級炭素 にしてしまったらどうでしょう。ネオペンタンからspiro[2.2]pentaneをつくるように結合を2本つくらせてできたのが、"spiro[2.2]octaplane"です。こうすると、最安定配座のδは3.1°まで減少しました。完全平面構造（エネルギー極大）との差は計算上10 kJmol^-1ていどに縮まっています。あと一息です。
　最後のだめ押しに、上下のシクロオクタン環2ヶ所を メチレン ブリッジでつなぎます。こうしてできたのが"dimethanospiro[2.2]octaplane"です（構造式をクリックするとChemscapeChimeで立体構造が表示できます、やり方は 第17話 を見てください）。こうすると計算上はδ0°になります。炭素間結合距離は最長（メチレンブリッジ部分）でも159.1 pm ですから、これまでに合成されている他の分子と比較しても無理な長さではありません。
　さて、実際にこの分子は合成できるのでしょうか？　どなたか挑戦してみてはいかがでしょう（笑）。

　cf. D.R.Rasmussen and L.Radom,Angew. Chem. Int. Ed.,1999,38, 2876.