鉄道模型おきらく研究室：レイアウトと列車のページ

'03/03/16	新設
'04/05/11	誤植訂正 勾配抵抗の式の誤りを田端機関区Ｄ５１さんの ご指摘で修正しました． 田端機関区Ｄ５１さんありがとうございました．

はじめに

レイアウトのプランを練るときに線路配置を決める必要がありますよね．線路配置を決める上で，走行性能に大きく影響するのは最大勾配と最小曲線半径です．最小通過半径は別項で扱うこととして，ここでは最大勾配について考えてみます．動力車だけなら楽々登れる勾配でも，トレーラーが多くなると空転して興ざめですし，ひどいときにはスリップして立ち往生したりしてしまうこともあります．ですから，レイアウトで運転したい列車の長さによって，最大勾配が違ってくるはずです．そこで車両の牽引力を測って，最大勾配を考察してみます．

初めてお読みになる方は最後のほうの「まとめ」から逆に，遡ってお読みください．

（'04/5/12追記）

田端機関区Ｄ５１さんの 走る蒸気機関車の模型を考える を合わせてお読みいただけると理解が深まります．大変な名文かつ，実物の豊富な知識裏付けされたご研究です．

第１段階：牽引力の測定

計測車両

下表の４台です．

車種	画像	メーカー	重量ｇｆ	備考
ＥＦ５８		ＫＡＴＯ	１２４
ＤＤ５１		ＫＡＴＯ	１１６
ＥＦ６６−１００		ＴＯＭＩＸ	１１７
７９６１８		MicroAce	６２	ゴム輪は第４動輪のみ

測定方法

摩擦係数（粘着係数）：傾斜法　　

まず，試験風景をご覧下さい．

図１　試験概要

レールの上に車両を乗せ，線路（TOMIX）を傾けます．傾斜が小さいうちは列車は空転せずに登りますが，傾きが大きくなると空転します．空転しない最大の勾配の角度をβ求めます．このとき車両に働く重力と牽引力とが釣り合っていますので，牽引力Fは

 　　　　　　　　　F=W Sin β
 　　　　　　　　　　　　　　　　で表せます．ここで，Wは車両の重量です．そこで，重量Wをはかりではかれば牽引力がわかります．（本来は，牽引力を荷重計などで直接測りたいのですが，資金不足なので上述の方法にしました．）
また，試験は前進だけおこないました．７９６１８は前後非対称なため，直進だけは両方向おこなって，後ほど補正します．

線路はＴＯＭＩＸを使いました．半径は次のとおりです．

・直線

・Ｒ３５４

・Ｒ３１７

・Ｒ２４３

測定結果

結果

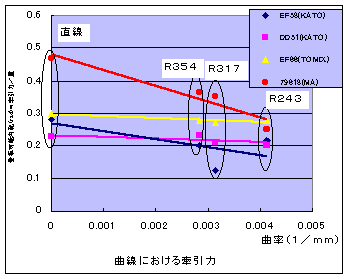
図２　登坂可能勾配（rad)

なお，７９６１８の登坂可能勾配が大きいのは前進で試験したためです．摩擦係数が大きいゴム輪が第４動輪だけにあるので，前進での坂を登るときのゴム輪の接地荷重は平坦で最大牽引力を発揮しているときよりも増えます（このような結果が出るのが勾配法の短所でしょうね）．そのため，登坂可能勾配が大きくなります．前向きと逆向きの登坂可能勾配の平均は０．４０です．

ところで，横軸を曲率（半径の逆数）にしています．この横軸のとりかたは実物をまねました．

図２の縦軸の値に重量をかけると牽引力になります．ただし，この牽引力は動輪周上のものですので，勾配では，動輪周上の牽引力から機関車の重さによる勾配抵抗分を引いたものがトレーラーを牽引する分の牽引力（引張棒牽引力）になります．

平坦直線路での計算結果が下の図です．

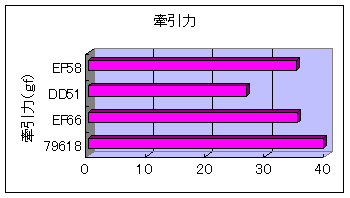
図３　平坦直線における牽引力（ｇｆ単位表示）

勾配や曲線上の牽引力も図２の縦軸に重量をかけれることでもとまります．ただし，この牽引力は動輪周上のものですので，勾配では機関車の重さによる勾配抵抗分を引いたものがトレーラーを牽引する分の牽引力（引張棒牽引力）になります．角度α（rad）における引張棒牽引力を式で書くと

引張棒牽引力

＝登坂可能勾配（β）×重量-α×重量

＝（β-α）×重量—————（０）

で求まります．

（ご参考：ｘ％勾配なら，α＝ｘ／１００radです）

ちなみに，牽引力の直線と曲線との比は下図のようになります．

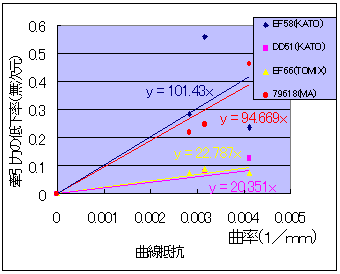
図４　曲線における牽引力の低下

上図中の式の係数を使うと，直線での牽引力にかかわらず曲線での牽引力の低下が直接比較できるので便利です．ＥＦ５８（ＫＡＴＯ）や７９６１８は２５０Rで約４割ほど牽引力が低下します．一方，ＥＦ６６（ＴＯＭＩＸ）やＤＤ５１（ＫＡＴＯ）の牽引力は１割の低下です．なお，図４の中の回帰式のｘの係数（ＥＦ５８なら１０１．４３）は曲線抵抗係数で単位はｍｍです．

曲線抵抗係数を使うと，牽引力は式（１）で表せます．

曲線や勾配における牽引力

＝直進登坂可能勾配（βo）×重量×（１−曲線抵抗係数×曲率）

＝直進登坂可能勾配（βo）×重量×（１−曲線抵抗係数／曲線半径）—————（１）

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（単位：ｇｆ）

第２段階：牽引定数

図３の横軸はｇｆ単位表示なんです（１ｇｆは１円玉にかかる重力と同じです）が，これではどの位の列車を引っ張れるのかわかりませんよね．そのためには，「ｇｆ」単位の代わりに「両」で牽引力をあらわすのが便利です．そこで国鉄やJRでは牽引力をあらわすのに牽引定数という方法をつかっています（ご存知の方も多いと思います）．これは重量１０ｔの仮想的な車両を想定して，これを何両牽引できるかであらわしたものです．牽引定数の一例をお示しします．

実物の牽引定数の例（単位：両）

	勾配
	１０‰	２０‰	２５‰
EF58	９０	５０	４０
DD51	１００	５５	４０

（ご参考：２０級の客車は，だいた２．５〜３両ぐらいに相当します．）

ちなみに，空積状態のワム８００００がちょうど，仮想車両１両（換算１両）に相当します．ですから，ＥＦ５８もＤＤ５１も２５‰ではワム８００００を４０両（現車４０両）牽引できることがわかります．また２０ｍ級客車は，仮想車両２．５〜３台分に相当します（換算２．５〜３両）ので，２５‰では牽引定数が換算４０両のＥＦ５８もＤＤ５１もブルトレ１４両（現車１４両）がやっとですね—————という具合に表現できるので牽引定数は便利です．そこで，このＨＰでは牽引力を牽引定数で表すことにします．

ところで勘違いしやすい？のですが，牽引力を１０ｔで割ったものが牽引定数ではありません．１０ｔの車両を引っ張る力ですので，牽引力を「１０ｔ車の走行抵抗」で割ったものが牽引定数になります．このことは勾配によって牽引定数が変わることでお分かり頂けると思います．

そのためには，１０ｔ車相当のトレーラーの平均的な抵抗を調べる必要があります．一番簡単な方法は実物で１０ｔ車に相当するワム８００００を模型でも１「両」にする方法ですが，実際に牽引するのは，２０ｍ級のボギー車であることが多いと思います．そこで２０ｍ級車両が２．５〜３「両」に相当するように，１０ｔ車相当の模型車両をきめます．

走行抵抗は，車重の影響が大きいでしょうから，まず，１７台の重量を調べてみました．

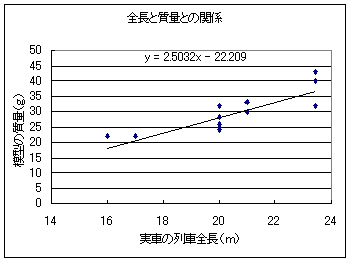
図５　車両の質量

上図の中の相関式から，２０ｍ級では２８ｇ前後が目安です．実際の２０ｍ級客車は，「１０ｔ車」２．５〜３台分ぐらいに相当するそうです．ですから，キリよく

「１０ｇの標準的な模型車両」を「１０ｔの実物車」

に見立てることにいたしましょう．

（余談ですが，ＴＯＭＩＸのワム８００００は８ｇでしたので，実車同様，ワム８００００は，ほぼ１「両」に相当します．）

くりかえしますと

１０ｇの仮想模型車両を１「両」と数える

ことにします．したがって，

１０ｇ車を何台引っ張れるかで牽引力を表す

ことになります．そのためには，１０ｇ車を引っ張るためにはどの位の力が必要か，言い換えれば１０ｇ車にどの位の抵抗があるのかを知る必要があります．

そこで，勾配法で計ってみました．線路を傾けても動き出さない最大の勾配の角度（rad)が抵抗係数になります．

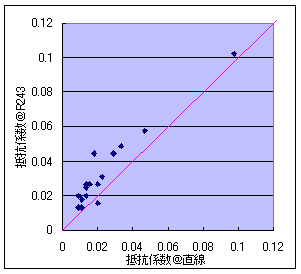
（参考図）線路を傾けても動き出さない最大の勾配の角度（rad)の直線と曲線における比較

まず直線での結果です．これは平坦な直線での発進抵抗係数に相当します．

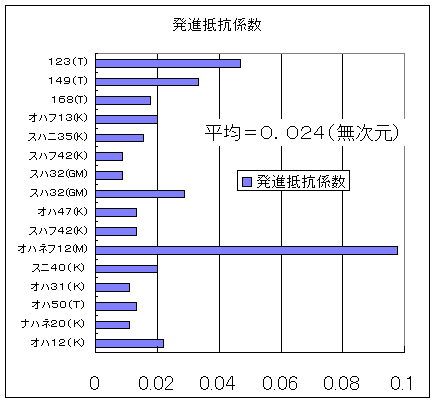
図６　発進抵抗係数

ここで

発進抵抗係数＝発進抵抗／車両重量

です．上図から発進抵抗係数の平均は０．０２４でした．そこで，丸めて

標準的な発進抵抗係数＝０．０２５

と決めました．

ところで，曲線では抵抗が増えます．そこでR243での発進勾配をもとめて，直進での発進勾配との差をとると，曲線での抵抗分が求まります．この値を曲率（＝1／２４３ｍｍ）で割って「曲線での抵抗の増加率」をもとめました（図３の式の係数に相当します）．その結果を下図にしめします．

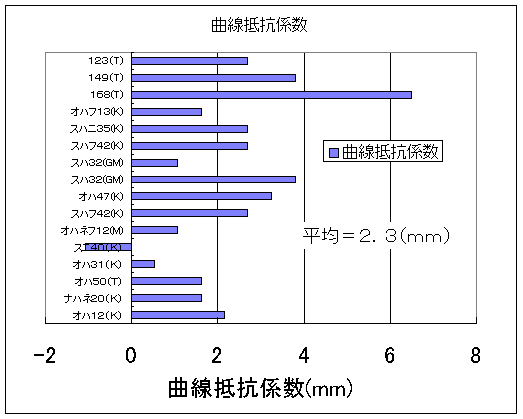
図６　曲線での抵抗増加 スニ４０の曲線抵抗係数が負になっていますが，おそらくこれは実験の繰り返し回数が少ないためだと思われます．何度も試験をくりかえせば，曲線抵抗の平均値は，正のある値に収束していくと思われます．ここでは，実験誤差の大きさの程度を知って頂くために，あえて再試験をしないで，負の値を示しています．

上の図の平均は２．３ｍｍです．そこでキリよく２．５ｍｍに丸めました．ですから

１０ｇ車の曲線抵抗係数　＝　２．５／曲線半径（ｍｍ）

と決めました．ですから，２５０Rを走行したことによる走行抵抗は車両重量の１％分で，これは勾配１％分に相当します．なお，図３の中の回帰式のｘ係数は機関車の曲線抵抗係数で，２０〜１００ｍｍぐらいですので，トレーラーの約１０〜５０倍ですですから，曲線による列車全体の走行抵抗はトレーラーよりも，機関車（動力車）のほうが多いようですね．

寄り道コーナー 専門書によると実物の曲線抵抗係数は 曲線抵抗係数＝０．６〜０．８ｍ／曲線半径（ｍ）だそうです（１）．ゲージ比で見るとＮゲージのほうが抵抗係数が小さいですね． Ｎゲージ ２．３ｍｍ／　９ｍｍ＝０．２６ 実物 ０．７ｍ／１．０６７ｍ＝０．６６ （１）天野ほか，図説鉄道工学Ｐ１１０，丸善出版，平成４年

さて，以上で走行抵抗を求める準備ができました．

（１０ｇ車）「１両」の走行抵抗つぎのようにして求まります．

・発進および平坦を走行しているときの抵抗＝発進抵抗係数×１０ｇf＝０．２５ｇｆ

・勾配の角度α（rad）における勾配抵抗＝α×１０ｇf

（ご参考：ｘ％勾配なら，α＝ｘ／１００です）

・曲線半径R（ｍｍ）における曲線抵抗＝曲線抵抗係数×１０ｇｆ／R＝２５／R　ｇｆ

したがって，上記を合計すると

走行抵抗＝０．２５＋１０α＋２５／R　ｇｆ—————（２）

となります．この計算例を下図にお示しします．

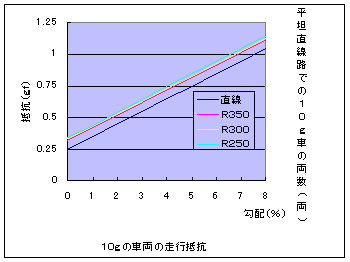
図７　１０ｇ車の走行抵抗

第３段階：測定結果の牽引定数表示

いよいよ機関車の牽引力を１０ｇ車に換算します．

（ここから読み始める方のためにご説明しますと，牽引力の単位がｇｆだと何両牽引できるかわかりにくいために，「（換算）両」の単位で表すことにします．大雑把には，ワム８００００を牽引できる両数で表し，これを「牽引定数」と呼ぶことにします．）

大雑把には，牽引定数とは，ある機関車がワム８００００を引ける両数のことです． ワム８００００画像

勾配や曲線における「１０ｇ車」の抵抗は式（２）でわかります．また，勾配や曲線における機関車の牽引力は式（１）でわかります．

したがって，勾配α(rad)，曲率半径Rにおける牽引定数は，牽引力を１０ｇ車の抵抗で割ったものですから

牽引定数＝（βo-α）×重量×（１−曲線抵抗係数／曲線半径）／（０．２５＋１０α＋２５／R）—————（３）

となります．ここで，βoは機関車の直進登坂可能最大勾配です．

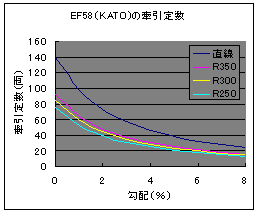
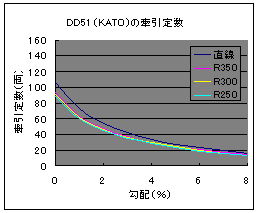
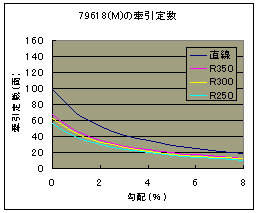
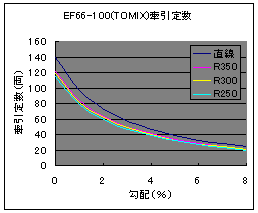
式（３）で計算した結果は次の通りです．

図８　機関車の牽引力

さて，曲線半径によって牽引定数が変わってきますので，ややこしく感じるかもしれません．大抵のレイアウトはエンドレスなので曲線があります．ですから，列車は曲線を通る必要があります．そのため，直線だけの牽引定数は直接の役には立たないので曲線における牽引定数だけを議論すればよろしいでしょう．どの曲線半径を用いるべきかは一概には言えませんが，厳し目の条件で牽引力を見積もったほうが良いと考えて，R250における牽引定数で議論することにします．下図は各機関車の牽引定数を比較した結果です．

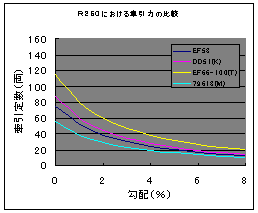
図９　牽引力の比較

なお図９の計算に用いた式は，式（３）にR=250（ｍｍ）を代入して求めた式（４）を使いました．

R2５０における牽引定数＝（βo-α）×重量×（１−曲線抵抗係数／２５０）／（０．３５＋１０α）—————（４）

ところで，上の図の牽引定数は平板の上で測定した結果です．しかし，勾配上のカーブで枕木を水平に設定すると線路がねじれます．そうすると３点支持台車でないかぎり垂直荷重が抜ける輪があります．摩擦が大きいゴム輪の荷重が抜けると牽引力がさがります．仮に４軸８輪にゴム輪が２輪の場合，１つのゴム輪の荷重が０になるとおよそ２割くらい牽引力が低下します．ですから他の要因も考えて牽引定数に３割の余裕を確保することにします（もうすこし実験を重ねて３割の余裕が妥当かを調べてみたいと思います）．

第４段階：あなたの列車が登れる勾配

それでは本題であるレイアウトの議論に入ります．

ケース１）長編成（トレーラー７両）の列車が登れる勾配

とりあえず，（現車）７両編成の客車を牽引させるとしましょう．そうすると客車１両が１０ｇ車約３両に相当しますので牽引定数２０両が必要です．そして余裕分の６両（換算）を加えると合計で牽引定数２６両になります．牽引定数２６両になる勾配は次のとおりです．

表　牽引定数２６両（現車７両）の勾配 勾配％ EF58 ３．９ DD51 ４．３ EF66 ５．９ ７９６１８ ２．４

７９６１８は別として，大型機であるEF58やDD５１クラスが，R250で実際の車両（現車）７両を安定して牽引できる限界の目安は４％あたりの勾配だと考えます．

ケース２）ローカル列車が登れる勾配

今度は７９６１８に客車（現車）２両を牽引させることを考えてみます．客車１両は１０ｇ車換算で約３両ですから，１０ｇ車６両分で，３割の余裕をみても高々８両です．どの機関車も８％勾配でしたら，（換算）２０「両」はあります．３割の余裕を見ると１４「両」ですので，２０ｍ級客車５両（現車）弱ぐらいに相当します．それでしたら，８％勾配でも余裕がありそうですね．

まとめ

ケース１とケース２をまとめると，

・長編成用のレイアウト（≒大型レイアウト）は最大勾配を小さく（トレーラー７両なら４％以下）したほうが良い，

・大型機が牽引するなら小編成用のレイアウト（≒小型レイアウト）では最大勾配を大きく（トレーラー２両なら８％）しても差し支えない

—————とまとめられそうです（当たり前のような気もしますが・・・・）．ですからレイアウトの記事のなかの「最大勾配」の数値を直接参考にすると危険です．むしろ「レイアウトの長さ×最大勾配」のような指標なら，サイズの影響をうけにくいので直接比較するのに便利そうですね．

おわりに

本来は牽引定数の計算結果を実験で検証したいのですが，手持ちの線路がありません．牽引定数の余裕を３割に丸めるなど，余裕を持たせすぎているような懸念があります．また，牽引力も本来は荷重計で測定したいところです．そこで，実験結果をお持ちの方がいいらっしゃいましたら，ご教示いただければ幸いです．また，精度の話のほかに，牽引力やトレーラーの測定例が十分ではありません．勾配法でもかまいませんので，測定結果をご提供頂けると幸いです．皆様の結果やご意見などがありましたら掲示板にどんどん書き込んでくださいね．

追記

（２００３年１１月４日追記）

牽引定数測定結果の追加

図９のデータ拡充のため 機関車データベース で調べた機関車について，牽引定数を算出しました．１１台のデータが追加されています．

なお，このときは簡便のために曲線抵抗係数をもとめないで，R２４３の曲線上における登坂可能最大勾配β'o(rad)を求め，次式で求めました．

牽引定数＝（β'o-α）×重量／（０．３５＋１０α）

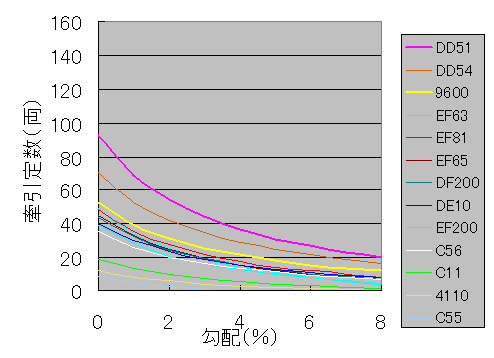
付図１　追加実験した牽引定数　 （図９と比較しやすいように，９６００とDD51は図９のものを再録してあります）

なお，R243をR２５０と考えています．

付図１から，９６００の牽引力は，付図１の中では平均よりも明らかに大きいことがわかります．

したがって，長編成の列車を５％勾配で安定して牽引できるのは，限られた機関車だけになりそうです．

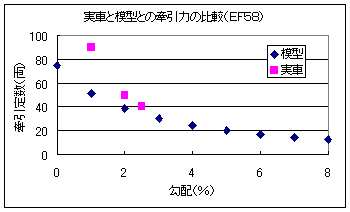
寄り道コーナー 実物と模型の牽引力を比較してみました． ＥＦ５８ 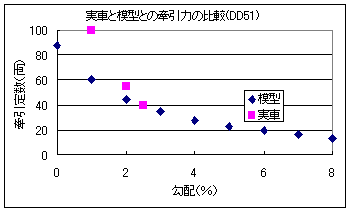ＤＤ５１ 実物の牽引定数は２５‰（２．５％）までしかわかりませんでした．２．５％までは実物のほうが長い列車が牽引できますが，２．５％以上の急勾配は模型のほうが長い列車を牽引できそうですね．ところで，実物は模型よりも右下がりですね．これは，実物は模型に比べて車輌重量で粘着力を稼いでいるためだと思います．そのため，勾配が大きくなると，機関車自体の勾配抵抗が模型に比べて大きくなります．したがって，実物の右下がりの度合いが模型よりも大きくなるんですね．